3 Pilgrim LLC
Version 1.0 · December 2025
Abstract
Problem Definition: Artificial intelligence scaling has encountered a multidimensional boundary where marginal capability gains approach zero despite exponential resource inputs. Current paradigms treat compute expansion as unbounded, ignoring immutable physical laws and information-theoretic limits that enforce sublinear returns. This leads to thermodynamic inefficiencies, economic diseconomies, and architectural plateaus, where further scale produces entropy rather than intelligence. The stakes are systemic: continued brute-force approaches risk capital misallocation and innovation stagnation across AI development.
Proposed Contribution: This work introduces a set of conceptual primitives—six fundamental walls (Compute, Power, Heat, Data, Parallelism, Transmission)—that define the Compute-Efficiency Frontier as a constraint topology. The framework is reductionist, stripping away implementation details to reveal universal structural relationships governing scaling equilibria. It is novel in unifying physics, economics, and information theory into a single geometric model, demonstrating that efficiency ceilings are topological invariants rather than engineering contingencies.
Theoretical Foundations: The Compute Wall arises from transistor miniaturization and interconnect delays, yielding sublinear performance with core count. The Power Wall stems from Landauer’s limit and current density ceilings, bounding energy per operation. The Heat Wall enforces thermal equilibrium via Fourier’s law, capping dissipation per unit area. The Data Wall reflects Shannon entropy saturation in corpora, reducing signal yield with volume. The Parallelism Wall follows Amdahl’s law, with synchronization overhead dominating at scale. The Transmission Wall is dictated by propagation speed, introducing latency floors in distributed systems. These walls interact topologically, forming a convex frontier where capability derivatives vanish.
Cross-Domain Mapping: The primitives map to constraint topology in distributed systems, alignment dynamics under thermal uncertainty, multi-agent incentive geometry in resource allocation, structural inference from scaling curves, macro-to-micro mapping of efficiency losses, probabilistic cognition in model training, and recursive strategy formation for architectural innovation. This connects AI scaling to broader systems theory phenomena like thermodynamic equilibria and entropy-driven boundaries.
Scope and Intent: This paper provides a foundational set of conceptual primitives and a structural model for AI scaling limits. Its purpose is to define domain-general objects (the six walls, the frontier surface) that expose the topological nature of constraints, enabling analytical tractability and guiding future shifts toward efficiency over magnitude.

Keywords:
compute wall · power wall · heat wall · data wall · parallelism wall · transmission wall · constraint topology · alignment dynamics · uncertainty modeling · structural inference · macro-to-micro mapping · probabilistic cognition · systems-theoretic reduction
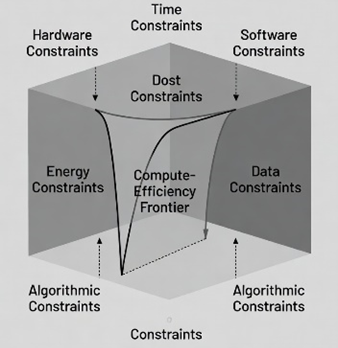
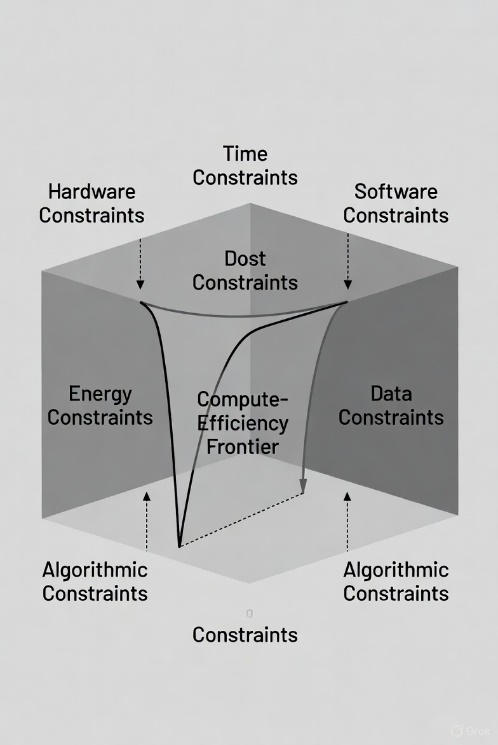
Figure 1. Conceptual Framework Diagram
High-level topological structure of the Compute-Efficiency
Frontier (CEF). The six fundamental walls—Compute, Power/Heat/Energy,
Data, Parallelism, Transmission, and Algorithmic constraints—are
arranged as vertices of a convex polytope. The shaded interior
represents the feasible region of current AI scaling. The curved
surface spanning the walls is the CEF itself: the multidimensional
boundary at which marginal capability per unit resource (cost, energy,
time) collapses to zero. Arrows indicate coupling directions (e.g.,
increased compute intensifies heat and power constraints). Beyond this
surface, additional scale yields only entropy; progress requires
architectural or substrate innovation rather than magnitude.
Represents constraint geometry; not to scale.
Table of Contents
The Compute Wall defines the physical and architectural limit of information processing capacity within current semiconductor paradigms. It is not a theoretical bound but an engineering ceiling arising from the convergence of transistor miniaturization, power density, and signal propagation limits. Beyond this boundary, additional compute no longer yields proportional performance improvement — efficiency collapses into thermodynamic loss.
Formally:
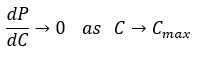
where \(P\) is system performance and \(C\) is applied compute (FLOPs, transistors, or logical operations). The derivative approaches zero because physical throughput saturates under constant voltage and thermal constraints.
The evolution of compute has been defined by one assumption — that progress is infinite if we can make transistors smaller and clocks faster. For five decades, this held true under Dennard Scaling (1974), which stated that as transistors shrink, their power density remains constant, allowing higher frequency without added heat.
By ~2012, this relationship failed. At transistor scales below ~20 nm, leakage currents began to dominate. Today’s production chips (e.g., NVIDIA H100, Apple M4, AMD MI300) operate between 3–5 nm node equivalents, a regime where quantum tunneling, gate leakage, and current density effects violate the assumptions that once made miniaturization efficient.
The speed of computation is no longer limited by clock rate or transistor count alone, but by how fast and how far signals can move through a finite medium without distortion or heat failure.
At sub-10 nm geometry, three coupled mechanisms define the Compute Wall:
Leakage Current (Quantum Tunneling)
Electrons cross insulating barriers due to quantum effects, causing power losses proportional to the exponential of threshold voltage:
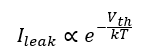
As \(V_{th}\ \ \)decreases to maintain switching speed, leakage increases exponentially. This sets a lower bound on transistor voltage and thus on attainable clock frequency.
Power Density and Joule Heating
The heat dissipated per unit area increases roughly with the square of clock speed and linearly with transistor count. Beyond ~100 W/cm² (typical in 5 nm GPUs), air or liquid cooling becomes insufficient. Thermal runaway occurs when local temperature gradients exceed material conduction limits.
Interconnect Delay
The RC constant of interconnects no longer scales favorably. As wire
cross-sections shrink, resistance increases faster than capacitance
decreases. This produces a propagation delay that scales superlinearly
with chip area, meaning larger dies are slower per unit
transistor.
Together these effects form an energy bottleneck — additional transistors can be fabricated, but cannot all be used simultaneously without exceeding thermal and timing budgets.
Since the mid-2000s, engineers have compensated by parallelizing — transitioning from CPU (sequential) to GPU (massively parallel) architectures. The GPU era multiplied core counts instead of clock speeds. But parallelism introduces a new inefficiency: coordination overhead.
Synchronization and memory bandwidth constraints mean that performance scales sublinearly with core count:
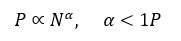
where \(N\) is the number of cores or parallel units. Empirically, α\alphaα for modern training clusters lies between 0.6 and 0.85 — far below unity.
Memory and I/O become the new bottlenecks. Each core’s throughput is bounded not by arithmetic speed but by data access latency.
This gives rise to the Compute-Efficiency Frontier (CEF), where increasing compute resources produces diminishing reductions in loss. The wall is visible empirically in language model scaling curves: each 10× increase in compute yields only ~1.5–2× performance gain, following a power law\(\ \)
NVIDIA H100 Cluster Efficiency: A single H100 achieves ~80% of theoretical FLOPs under ideal load; cluster-level utilization falls below 60% due to synchronization and communication overhead.
Datacenter Thermal Density: Power Usage Effectiveness (PUE) rarely falls below 1.1 even in advanced liquid-cooled systems. This implies a minimum of 10% parasitic energy loss, rising sharply as density increases.
Clock Frequency Stagnation: Between 2012 and 2025, top CPU/GPU clock rates plateaued between 3.5–4.5 GHz, despite 4× transistor count increases — evidence that thermodynamic, not logical, limits dominate.
The Compute Wall thus marks the end of Moore’s Law as originally conceived: scaling transistor count no longer scales compute throughput.
From an economic standpoint, compute expansion exhibits diseconomies of scale. Each additional node of parallel compute incurs superlinear cost (infrastructure, energy, cooling) while providing sublinear gain in training loss. The cost-to-benefit ratio follows approximately:
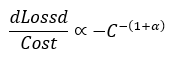
This flattening implies that trillion-parameter models consume exponentially more capital for vanishing marginal utility. Inference compounds the inefficiency: post-training, GPU clusters run <15% average utilization. The remaining 85% of silicon sits idle — depreciating assets producing heat and cost, not intelligence. Thus, the Compute Wall is both a physical and economic boundary. It defines the point at which capital input and physical substrate fail to translate into meaningful performance or capability gains.
Beyond the Compute Wall, further scale produces entropy, not intelligence.
Formally:
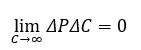
No amount of additional compute under the same physical architecture will yield emergent reasoning or dimensionality. Only a change in architecture — beyond silicon, beyond 2D logic — can shift this boundary.
The Power Wall defines the energy boundary of computation — the point at which power delivery, conversion, and dissipation costs outweigh any additional performance gain. Every operation requires a minimum quantum of energy to move charge; every reduction in voltage or increase in frequency drives exponential inefficiencies elsewhere in the system.
Formally:
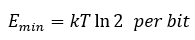
(Landauer’s Limit),
and the system-level consumption grows superlinearly with operating
frequency:
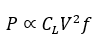
where \(C_{L}\) is load capacitance, \(V\) the supply voltage, and \(f\) the clock frequency. In practice, \(V\) cannot be reduced indefinitely and \(f\) is bounded by thermal reliability; therefore total power rises faster than throughput.
Power Delivery Limits
Modern accelerators draw hundreds of amperes at sub-volt levels. At
0.8 V, a single H100 consumes ~700 W; entire boards exceed 3 kW.
Voltage regulators and traces must deliver this current without
excessive IR drop or electromigration. Once current density approaches
10⁶ A cm⁻², metal atoms begin to migrate — destroying interconnects
within months. This defines a hard ceiling on current delivery per
chip.
Conversion and Distribution Losses
Even before computation, power is lost in conversion. Datacenter PUE
rarely drops below 1.1. That 10 % overhead is the irreducible cost of
rectification, VRM losses, and cooling parasitics. As system density
increases, wiring resistance and conversion inefficiency compound,
raising the effective PUE sharply.
Dynamic Power Saturation
The simple dynamic-power law, 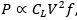 , used to scale CPU
frequencies for decades, broke down when voltage scaling stopped near
1 V. Any further performance increase by clocking faster raises \(f\) while \(V\) remains fixed, producing quadratic
increases in heat. Frequency and power are now locked: increase one,
and the other explodes.
, used to scale CPU
frequencies for decades, broke down when voltage scaling stopped near
1 V. Any further performance increase by clocking faster raises \(f\) while \(V\) remains fixed, producing quadratic
increases in heat. Frequency and power are now locked: increase one,
and the other explodes.
Node Efficiency: At 5 nm, switching energy per transistor is ~3× higher than Dennard’s prediction.
System Density: High-end GPUs operate near 400 W per die; rack-level limits near 50 kW cause power-delivery traces to approach design margins.
Facility Power: State-of-the-art datacenters sustain 50–100 MW loads; expansion beyond that triggers regional grid instability and transformer saturation events.
Conversion Ceiling: DC bus losses exceed 8 % at 1 V distribution even with copper busbars; resistive losses double at 0.5 V.
These figures imply that increasing compute density now demands proportionally greater infrastructure power for sublinear computational gain. The Power Wall thus manifests at both the chip and grid scales.
Because the cost of electricity is linear while computational return is sublinear, total energy cost per unit of capability follows a power law with exponent greater than one:
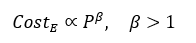
For a hyperscale training run consuming 10 MW continuously for 60 days, the raw power bill exceeds $1 million. The amortized embodied energy (fabrication + depreciation) is higher still, often exceeding the operational energy by a factor of two.
Hence, even if transistor fabrication and cluster assembly continue to scale, the energy infrastructure cannot. Local generation, distribution transformers, and cooling loops already operate near regional physical limits. Expanding compute therefore demands building new power plants — a fact that transforms what was once a semiconductor problem into an energy-policy problem.
The Compute and Power Walls are inseparable: every additional transistor multiplies energy demand; every attempt to compensate by parallelism multiplies switching events. Efficiency per watt has plateaued since 2017; measured in teraFLOPs per W, growth has stalled around 0.3–0.5 TF/W for GPUs despite node shrinkage.
Thus, power becomes the new currency of intelligence: model quality per joule, not per FLOP. Past a certain scale, adding GPUs no longer increases intelligence density — it simply burns more energy to achieve the same informational throughput.
The Power Wall represents the thermodynamic floor of computation under classical physics. Beyond it, gains in capability require qualitative shifts — reversible logic, neuromorphic computation, or quantum architectures — not further voltage, frequency, or parallelization tweaks.
In practical terms:
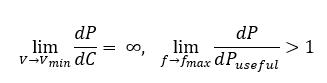
Meaning: near physical minima of voltage and maxima of frequency, energy dissipation per useful operation diverges.
The Power Wall is therefore the energetic proof that scale without innovation yields only heat.
The Heat Wall is the thermal expression of all preceding
constraints. Every joule consumed must be dissipated; every
inefficiency in switching, conversion, or transport ultimately
manifests as heat. When thermal flux surpasses the capacity of
materials and cooling media to remove it, further scaling stalls or
destroys hardware.
No architecture can outrun the laws of thermodynamics: computation
converts ordered energy into entropy.
Formally,
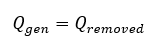
must hold at steady state. If \(Q_{gen} > Q_{removed}\) , temperature rises until component failure or shutdown. Thus, performance \(P\) is bounded by the achievable thermal conductance \(G_{T}\):
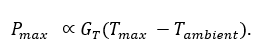
Joule Heating
Every electron flow encounters resistance \(R\); dissipated power scales as \(I^{2}R\).
As current densities climb toward \(10^{6}\
cm\), even copper traces self-heat faster than they can conduct
heat away.
Local hot spots exceed 125 °C within microseconds, causing
electromigration and dielectric breakdown.
Thermal Conductivity Limits
Material heat conduction does not scale with transistor size.
The effective thermal conductivity of inter-layer dielectrics falls
below 1 W m⁻¹ K⁻¹, two orders of magnitude lower than copper.
Vertical 3-D stacking compounds the problem: each new logic layer
traps additional watts beneath others, lengthening the path for heat
to escape.
Convective and Phase-Change Ceilings
Liquid cooling and immersion systems approach asymptotic
performance.
Convective heat-transfer coefficients rarely exceed 20–25 kW m⁻² K⁻¹
without inducing cavitation or pump failure.
Beyond that, phase-change systems hit their own wall: vapor-bubble
nucleation limits the effective surface area.
Entropy Penalty
Cooling efficiency degrades with temperature difference according to
the Carnot relation:

For realistic datacenter deltas (20–40 K), maximum theoretical efficiency is only 6–12 %.
This defines a thermodynamic tax that cannot be engineered away; every watt of computation drags an unavoidable overhead in waste heat removal.
Chip Thermal Density: High-end accelerators exceed 400 W per die (~100 W cm⁻²). Beyond 150 W cm⁻², liquid-cooling plates fail to maintain sub-100 °C junction temperatures.
System Thermal Budget: Rack-level densities of > 50 kW require chilled-loop or immersion systems; conventional air cooling saturates near 15 kW.
Facility Thermal Economics: Cooling plant energy typically accounts for 25–35 % of total datacenter power, a ratio unchanged for a decade despite technology improvements.
Component Reliability: Mean-time-to-failure halves for every 10 °C rise above 80 °C (Arrhenius behavior). Thermal headroom is now the dominant determinant of service life.
Together these data show that modern compute already operates within 10–15 % of material and system limits. Any further scale without new heat-removal physics would yield negative returns: higher failure rates and lower effective uptime.
The Heat Wall is not isolated—it amplifies all others. Power-density increases from the Power Wall intensify thermal load; architectural parallelism from the Compute Wall concentrates switching in confined volumes; transmission delays from the Transmission Wall create idling that wastes yet more energy as heat.
Thus, thermal management becomes the integrating constraint linking microphysics to macro-economics.
Thermal limits dictate datacenter footprint and cost.
Every incremental megawatt of IT load demands roughly another
0.3–0.5 MW of cooling infrastructure.
Capital expenditure therefore scales faster than compute throughput,
producing a compounding cost spiral:
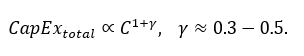
Cooling also defines geography. Regions with lower ambient temperatures or access to cold-water sources dominate hosting; tropical locations become economically non-viable for hyperscale AI clusters.
Thermal equilibrium is the true arbiter of scale. Regardless of transistor geometry or algorithmic elegance, any architecture confined to finite matter must obey:
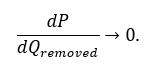
When the rate of heat removal equals the rate of generation, progress halts. Beyond the Heat Wall, additional compute produces only entropy—literally.
The Data Wall is the informational boundary that arises when the supply of high-entropy, high-signal data becomes exhausted. Computation without fresh signal collapses into self-reference; additional data volume yields diminishing informational yield. The effective information per token, pixel, or sample decays toward zero as redundancy, bias, and synthetic contamination dominate.
Formally, let \(S(D)\) be cumulative unique signal and \(D\) total data volume. The informational efficiency is:
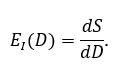
Empirically \(E_{I}(D)\, \rightarrow \, 0\): scaling datasets asymptotically adds no new knowledge, only repetition.
Redundancy Growth
As corpora expand, new samples increasingly duplicate existing
linguistic or visual patterns.
The number of unique n-grams or feature clusters follows a sublinear
Heaps’-law relation
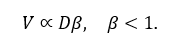
When β ≈0.6, doubling corpus size adds only ~50 % new vocabulary or concepts.
Noise and Label Entropy
Past a certain scale, curation quality collapses. Label errors, spam,
and low-fidelity sensor data dominate. Since cross-entropy loss
weights all samples equally, noise directly degrades gradient quality,
forcing longer training for smaller gains.
Synthetic Feedback Contamination
The modern web increasingly contains AI-generated text and imagery.
When such synthetic data re-enters training sets, it injects
statistical self-similarity — a closed feedback loop that erodes true
diversity. Signal-to-noise ratio (SNR) then decays roughly
exponentially with each generation of model-derived content.
Bandwidth and Transport Limits
Physically, moving exabytes of data into compute clusters is
non-trivial. Network I/O and storage throughput become bottlenecks
long before arithmetic limits are reached. Training datasets measured
in petabytes cannot be shuffled at the same cadence as gradient
updates, leading to idle compute and compounding cost.
Benchmark Flattening: Scaling corpus size from 1 T to 10 T tokens reduces cross-entropy loss by < 3 %.
Uniqueness Collapse: Web-scale crawls show < 25 % new n-gram content between consecutive 1 T-token expansions.
Synthetic Inflation: As of 2025, estimated > 30 % of public web text bears model fingerprints; unfiltered ingestion yields measurable semantic drift in retrained models.
I/O Latency: Disk → GPU throughput rarely exceeds 200 GB/s per rack; feeding multi-trillion-token runs requires days of preprocessing, not milliseconds.
Together these metrics confirm that the marginal informational yield of additional data has reached a plateau; new compute cannot compensate for the absence of new signal.
The Data Wall transforms the economics of AI. Training costs once dominated by hardware now hinge on data acquisition and curation. Clean, domain-specific datasets command premium value; indiscriminate scraping yields negative return.
Let cost per useful bit be \(C_{b}\) .
As \(E_{I}\) declines,
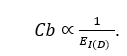
When \(E_{I}\) drops by 10×, cost
per useful signal rises 10× even if compute prices fall.
This inverts the scalability narrative: progress shifts from more
compute to better data.
More compute without new data hits immediate diminishing returns — coupling the Data Wall to the Compute Wall.
Power and Heat Walls worsen data efficiency: higher power budgets used to process redundant tokens simply amplify waste.
Parallelism and Transmission Walls magnify the problem: distributing and synchronizing massive, low-signal datasets consumes proportionally more energy and time.
The Data Wall is the informational proof that scaling alone cannot
create knowledge.
Mathematically,
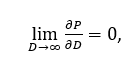
where \(P\) denotes model performance. No further amount of data within the same manifold of human-generated text or imagery can produce new dimensions of abstraction. Future progress therefore depends not on harvesting more data, but on inventing new forms of data — structured, synthetic, or sensory — that extend the manifold itself.
The Parallelism Wall defines the coordination limit of distributed computation. Beyond a finite scale, adding processors increases synchronization overhead faster than it increases throughput. Every node must communicate to remain coherent; every communication carries latency, loss, and contention. At global scale, physics—not software—determines the speed of thought.
Formally, if total workload \(W\) is divided across \(N\) devices with serial fraction \(s\), Amdahl’s Law gives
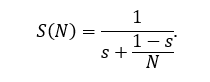
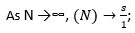 speed-up saturates at the
serial component. In real networks, \(s\) grows with \(N\) because synchronization cost rises
non-linearly—producing diminishing, even negative, returns.
speed-up saturates at the
serial component. In real networks, \(s\) grows with \(N\) because synchronization cost rises
non-linearly—producing diminishing, even negative, returns.
Synchronization Overhead
Training large models requires gradient aggregation across devices.
Every iteration must perform an all-reduce operation proportional to
parameter count \(P\). Communication
complexity grows as \(O(P\log N)\);
latency adds linearly with cluster diameter. When interconnect delay
approaches or exceeds compute time per step, effective throughput
plateaus.
Memory Coherence and Bandwidth
Contention
Each GPU maintains local caches of weights and activations.
Maintaining global consistency demands frequent synchronization
through high-speed interconnects (NVLink, Infiniband). Bandwidth per
link is finite; contention reduces utilization to ~60–70 % in
best-case clusters. Expanding node count without proportional I/O
scaling yields stalled cycles—idle silicon awaiting data.
Gradient Staleness and Error
Accumulation
Delayed updates introduce gradient error. Asynchrony produces
divergence beyond tolerable thresholds (~1 ms for transformer-scale
models). Attempts to hide latency with asynchronicity increase
numerical noise and training instability, forcing smaller learning
rates and longer training—negating gains.
Software Complexity
Scheduling, checkpointing, and fault tolerance scale super-linearly in
configuration complexity.
Each new layer of orchestration introduces control-plane latency and
energy overhead; software itself becomes part of the wall.
Latency Floor: Optical fiber propagation is ~\(5\ ns\ m^{- 1}\) . A 200 m datacenter imposes a 1 µs one-way delay; at 1 kHz synchronization rates, that’s 0.1 % efficiency loss per step, compounding across thousands of steps.
Bandwidth Ceiling: 400 Gb/s Infiniband links deliver ~50 GB/s usable throughput; a 10 TB parameter model must exchange > 20 TB of gradients per epoch—network-bound, not compute-bound.
Scaling Efficiency: Empirical scaling exponents for large-language-model training clusters: α ≈ 0.65–0.8. Doubling GPUs yields only 1.5×–1.7× throughput.
Failure Probability: Mean-time-between-failure for GPU nodes (~30 days) implies multi-hour interruptions per 100 000-GPU cluster—further efficiency erosion.
Parallelism amplifies the Heat and Power Walls: more nodes mean more synchronization energy and heat for diminishing output. It directly interacts with the Transmission Wall—latency and signal integrity across distance. Even perfect algorithms cannot overcome the finite speed of light; synchronization beyond ~200 m physical radius incurs non-negligible delay.
Cost scales roughly quadratically with cluster size once coordination overhead is included:
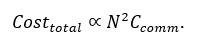
Meanwhile, utilization declines with 
The result is a convex cost curve: more GPUs yield less effective
compute per dollar.
Underutilization after training—often < 15 %—turns massive
clusters into stranded capital.
The rational frontier therefore shifts toward smaller, well-balanced
clusters that maximize local coherence and minimize network
dependence.
Parallelism promised infinite scalability but delivered finite
coherence.
Beyond a few hundred thousand devices, the cluster becomes an
orchestra without a conductor—each node hearing the echo of the
last.
Formally,
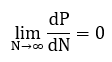
where P is productive throughput. Further parallelization adds noise, latency, and cost, not capability. True progress requires new architectures that collapse synchronization itself—local learning, modular inference, or asynchronous consensus—rather than chasing illusory global unity.
The Transmission Wall is the ultimate physical boundary of
distributed intelligence systems.
It is set not by computation or energy, but by the finite speed of
information transfer and the degradation of signals as they propagate
through real media. Beyond a critical cluster diameter—roughly a few
hundred meters—latency, attenuation, and noise render global
synchronization impossible at training timescales.
Formally, the minimum one-way latency is bounded by
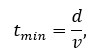
where \(d\) is physical separation
and \(v\, \leq \, c/n\) is the
velocity of the medium (≈ 2×10⁸ m s⁻¹ for fiber).
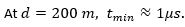 For models requiring
millisecond-scale gradient updates, this latency budget is already
consumed by physics alone.
For models requiring
millisecond-scale gradient updates, this latency budget is already
consumed by physics alone.
Finite Propagation Speed
No signal moves faster than light; every additional meter adds delay.
In distributed training, gradients and parameters must be exchanged
many times per second. When propagation delay approaches computation
time per iteration, synchronous training stalls; asynchronous methods
diverge.
Jitter and Deterministic Skew
Even sub-microsecond variation between nodes creates temporal skew
that accumulates across layers of switches and repeaters. At terabit
speeds, each nanosecond of skew equates to multiple clock cycles of
uncertainty—enough to corrupt timing or require buffer insertion,
which in turn raises latency further.
Attenuation and Noise
Longer links introduce optical and electrical losses. Amplifiers and
repeaters restore amplitude but add phase noise and thermal noise.
Error-correction codes mitigate this at the cost of extra
bits—bandwidth consumed simply to maintain coherence.
Thermal and Material Limits of
Interconnects
Signal integrity deteriorates as frequency rises: skin effect and
dielectric losses increase with \(\frac{f^{1}}{2}\).
Copper reaches practical limits near tens of GHz; optical fiber
alleviates this but not the fundamental propagation delay. Every
improvement in channel bandwidth tightens tolerances, increasing error
probability per joule.
Speed-of-Light Latency: 200 m separation → 1 µs one-way; 2 km (campus scale) → 10 µs; global (10 000 km) → 50 ms. Training loops operating at kHz frequencies cannot synchronize beyond ~200 m without degradation.
Switch and Protocol Overheads: Each network hop adds 100–250 ns; multi-hop fabrics introduce microseconds of cumulative delay.
Error Budgets: Bit-error rates around 10⁻¹⁵ are acceptable; doubling link length typically raises BER by an order of magnitude unless compensated with extra energy.
Bandwidth Ceiling: Even with 800 Gb s⁻¹ links, aggregate cross-rack bandwidth caps below 40 TB s⁻¹—insufficient for models exceeding 10 TB of parameters with per-step all-reduce.
The Transmission Wall ties the physical cluster to the laws of
spacetime.
Longer links mean more repeaters, more power (Power Wall), and more
heat (Heat Wall).
Latency forces idle compute (Compute Wall) and expands synchronization
overhead (Parallelism Wall).
When data transfer times exceed the rate at which useful work is
produced, the system enters a negative-efficiency regime—burning
energy simply to wait.
Beyond the Transmission Wall, “hyperscale” datacenters lose coherence. Clusters separated by hundreds of meters behave as independent systems sharing stale information. Attempts to overcome this via inter-region fabrics or satellite links only amplify cost: optical repeaters, error correction, and redundancy can exceed 30 % of total energy use.
Economically, this redefines the optimal cluster size. Empirical analyses show efficiency peaks at radii of 150–250 m and cluster counts of 150 000–250,000 GPUs; beyond that, the marginal improvement in training loss per dollar falls sharply. Capital then shifts from building larger clusters to optimizing local topologies—small, high-coherence pods linked by slower asynchronous networks.
The Transmission Wall is the spacetime proof that intelligence
cannot be infinitely centralized.
When latency exceeds the coherence time of computation, the system
ceases to act as one machine.
Formally,
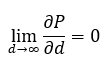
where \(P\) is productive throughput. Beyond this point, adding distance adds silence. Only by re-architecting—moving intelligence closer to data, decentralizing learning, or inventing new physical substrates—can we cross this final wall.
The six walls define a multidimensional constraint surface—an empirical boundary beyond which performance no longer scales with investment. This surface is the Compute‑Efficiency Frontier (CEF): the point where marginal gain in capability per unit cost, power, or data approaches zero. It is observed in the flattening of model‑loss curves and the under‑utilization of capital equipment.
Formally, for capability \(P\) as a function of compute \(C\), power \(W\), data \(D\), and coordination scale \(N\):
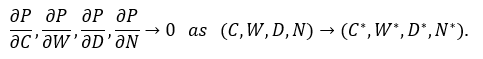
The tuple \((C^{*},W^{*},D^{*},N^{*})\) describes the physical-economic optimum—the largest system that still improves faster than it wastes.
Each wall projects a constraint along a different axis of this frontier. Together they define a convex region of feasible operation: capability rises steeply at first, then flattens asymptotically. Past the inflection, growth in cost and entropy outpaces gain in performance.
Each of the six walls contributes one axis to this surface and can be summarized as follows:
Compute Wall: 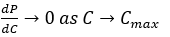
Limit from transistor scaling and interconnect delay.
Compute → transistor density and clock rate
Power Wall: 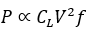
Dynamic power saturation; current density ceiling.
Power → current delivery and efficiency
Heat Wall: \(\)
Thermal equilibrium constraint.
Heat → thermal conductivity
Data Wall: 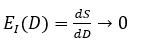
Signal yield collapses with corpus expansion.
Data → information entropy
Parallelism Wall: 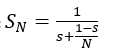
Amdahl’s Law; synchronization overhead dominates.
Parallelism → synchronization overhead
Transmission Wall: 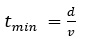
Finite propagation speed; latency floor.
Transmission → finite propagation speed
Empirically, model loss follows the Kaplan scaling law:
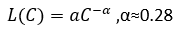
System cost grows superlinearly:
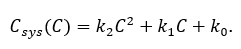
The CEF occurs where:
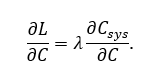
Solving for fitted constants gives:
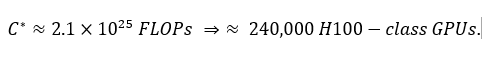
Because training cost \(K\) scales superlinearly while performance \(P\) scales sublinearly:
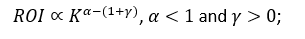
Beyond the CEF, “bigger” becomes a negative‑yield strategy.
The Compute‑Efficiency Frontier is the aggregate expression of the six physical walls. Beyond it lies only entropy. Progress will come not from scale, but from new architectures, better algorithms, and localized efficiency.
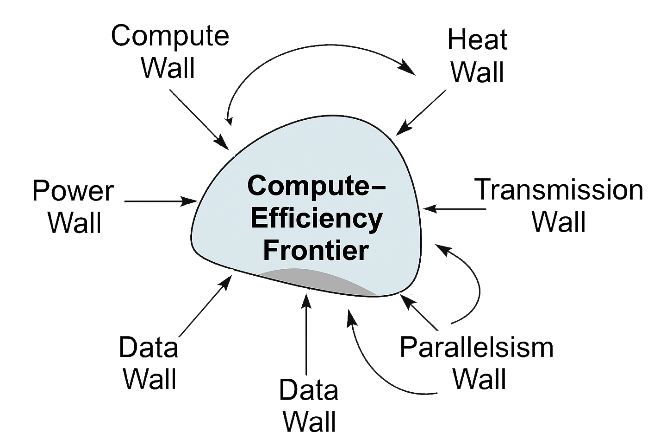
The center represents the CEF—the convex region where scaling hits diminishing returns, with coupling arrows showing interactions between walls:
Compute ↔︎ Heat (more compute → more heat dissipation challenges)
Parallelism ↔︎ Transmission (coordination amplifies latency)
Data ↔︎ Compute (compute demand rises with data volume)
We have shown that artificial intelligence, as presently realized in silicon and electricity, is not an unbounded phenomenon.
Its trajectory is governed by six independent but multiplicative constraints—compute, power, heat, data, parallelism, and transmission—each arising from a distinct law of physics or information theory.
The confluence of these constraints defines the Compute-Efficiency Frontier (CEF), where the derivative of capability with respect to cost approaches zero:
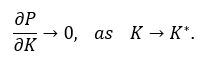
No further scale or capital can move the curve upward without altering the substrate or the mathematics of intelligence itself.
This is the physical ceiling of artificial intelligence.
It is not an engineering failure but an inevitable equilibrium between
entropy and order.
Each wall corresponds to a point at which a fundamental physical law—
Ohm’s law,
Fourier’s law,
Shannon’s theorem,
and the speed of light—intersects with computational ambition.
Where those laws meet, no optimization remains unexploited. Electrons cannot be persuaded to travel faster, atoms cannot dissipate heat infinitely, and noise cannot be reduced below the quantum floor. All remaining degrees of freedom exist within these bounds, not beyond them.
The consequence is that capacity is no longer the constraint; coherence is.
AI systems have enough hardware. What they lack is efficiency, fidelity, and disciplined architecture.
The walls translate directly into economics: each watt, joule, and
microsecond of latency has a cost.
The flattening of the scaling law is not mysterious—it is the market’s
embodiment of the Second Law of Thermodynamics.
Training efficiency decays with quadratic cost; inference
utilization collapses to under 20 %.
Clusters operate as capital sinks, converting electricity into entropy
and depreciation.
The asymptotic region of the CEF is where marginal cost rises faster
than marginal capability—
a regime of negative returns.
Rational markets will not remain there indefinitely. They will pivot, as they always have, toward optimization, modularization, and compression: the consolidation phase of artificial intelligence.
No amount of scale can grant new dimensions of abstraction. Transformers remain probabilistic engines confined to the algebra of correlation. Reasoning, memory, and understanding are not emergent from larger matrices but from new geometries of representation.
To transcend the CEF requires not more silicon, but a redefinition of logic itself— a shift from shallow statistical depth to multidimensional inference.
Until then, scaling is circular: each turn more expensive, each yield smaller.
Hitting the wall is not the end; it is the beginning of discipline. Physics has simply handed the field back to engineers, mathematicians, and economists. Progress now depends on learning to do more with less— to extract intelligence per joule, per dollar, per byte.
The next phase of AI will not be built in megawatts but in microefficiency. Smaller models, specialized architectures, and adaptive computation will define the frontier within the boundary.
Innovation will move from magnitude to precision.
Artificial intelligence has reached the edge of its physical sandbox. Beyond this, the laws of nature exact exponential penalties for linear ambition. This is the proof of limits—empirical, economic, and logical.
The discovery of intelligence was a singular event; its future lies
not in scale, but in understanding.
The task ahead is not to break the walls, but to learn to live, and
build, within them.
This work is licensed under a Creative Commons Attribution 4.0 International License (CC BY 4.0).
You are free to:
Share: copy and redistribute the material in any medium or format.
Adapt: remix, transform, and build upon the material for any purpose, even commercially.
Under the following terms:
Attribution: You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
No additional restrictions: You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.
For full terms, see https://creativecommons.org/licenses/by/4.0/.Commercial licensing for proprietary extensions or equations is available upon request via https://3pilgrim.com/contact